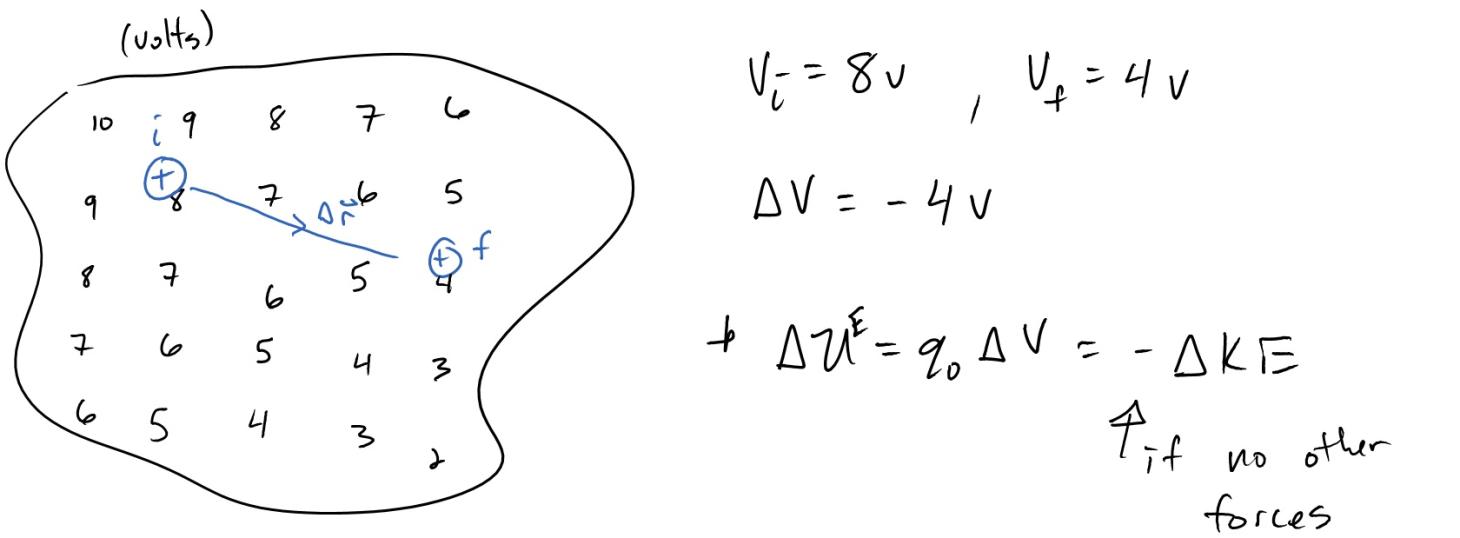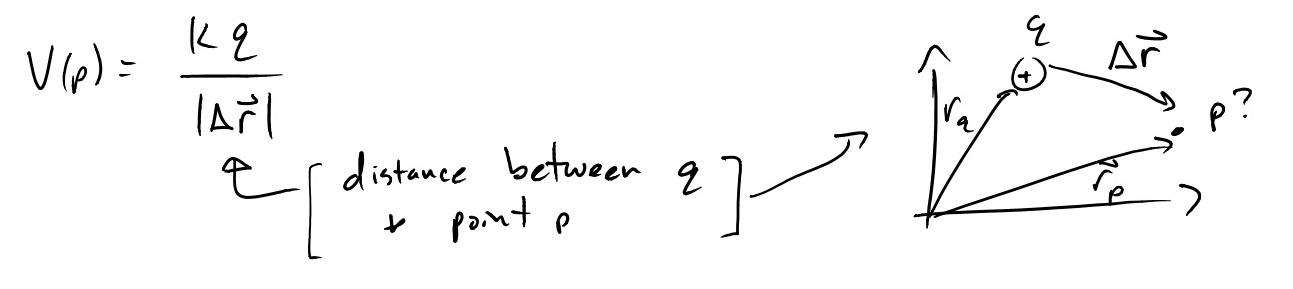Electric Potential | Electric Potential Energy
Lets recall the concept of a field.
Things create fields that alter the space around them in such a way that facilitates interactions with other things. The field is owned by the original thing and in that way precludes the existence of the second thing and any interactions that may occur between the two.
We've learned about how the electric field can be used to describe force interactions. The concept is that the first charged particle $A$ creates an electric field $\overrightarrow{E}_{A}$ that the second test charged particle $O$ resides in. Particle $O$ then feels a force $\overrightarrow{F_O}$ equal to the charge of $O$ ($q_O$), multiplied by the electric field of $A$.
$\overrightarrow{F}_O=q_O \overrightarrow{E}_A$
The electric potential $V$ is connected the electric potential energy $U$ in a similar way. The electric potential is the field created by charge $A$ that test charge $q_O$ resides in. The potential energy of the system is then the charge $q_O$, multiplied by the electric potential from $A$.
$U_{OA} = q_O V_A$
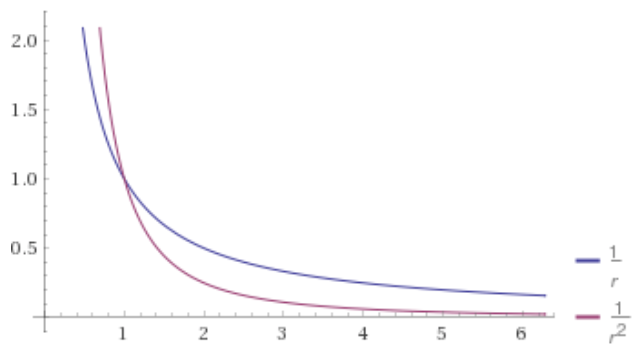
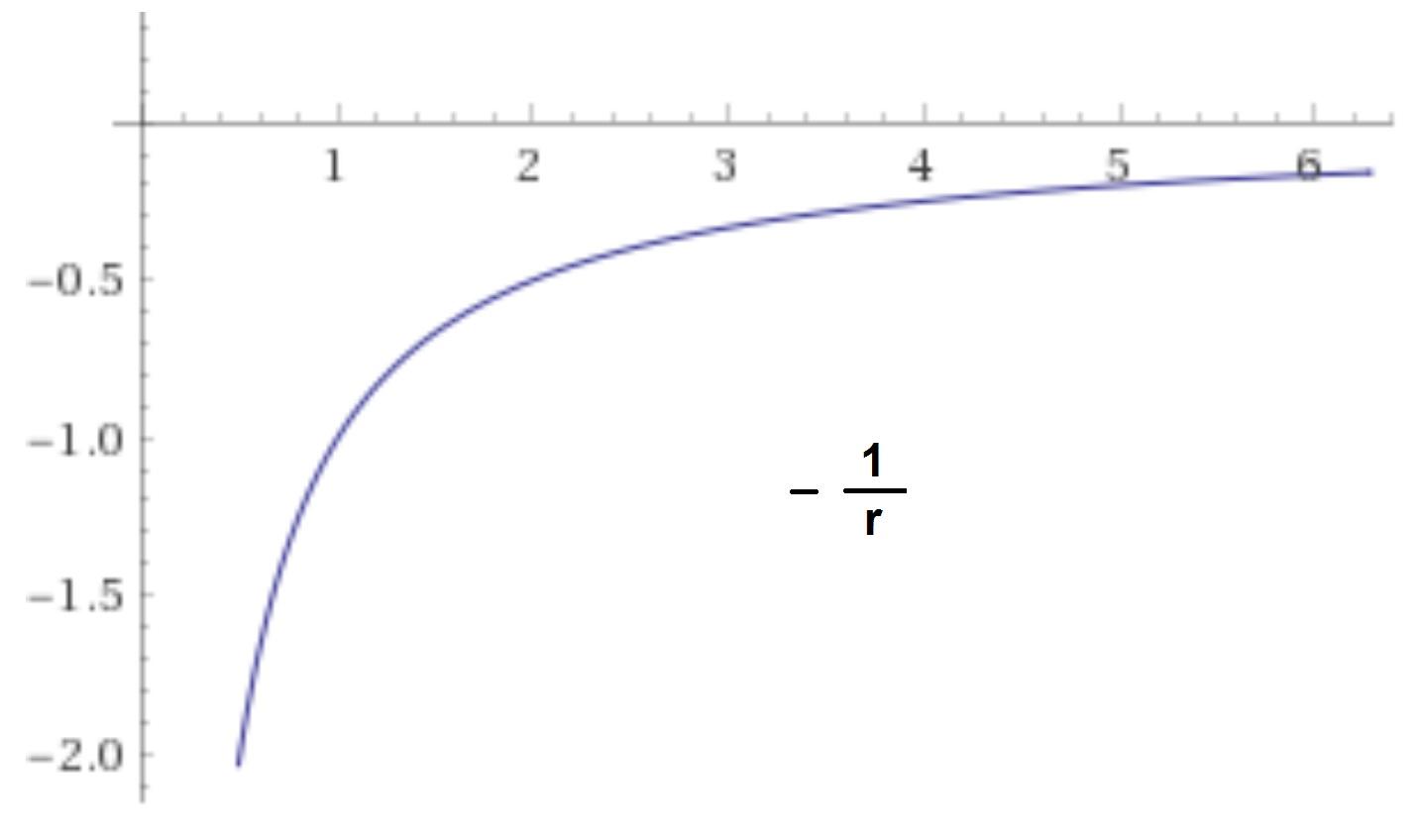
Recall that energy is a scalar quantity and so is the charge of a particle. That means that the electric potential $V$ must also be a scalar. The electric potential is a scalar field, it's a number at every point in space. It is used to describe how a charged particle alters the space around them (in an abstract way) and is used to quantify the potential energy between the charge originating the field and those residing in the field. Pulling from the example in the Overview, we know that if two protons are next to each other they will repel one another and speed up. They will increase their kinetic energy as they both move towards the state with a minimum of potential energy, a state far away from each other. This is all due to the interaction between them - the electric potential is the field we use to describe the interaction with an energy analysis.
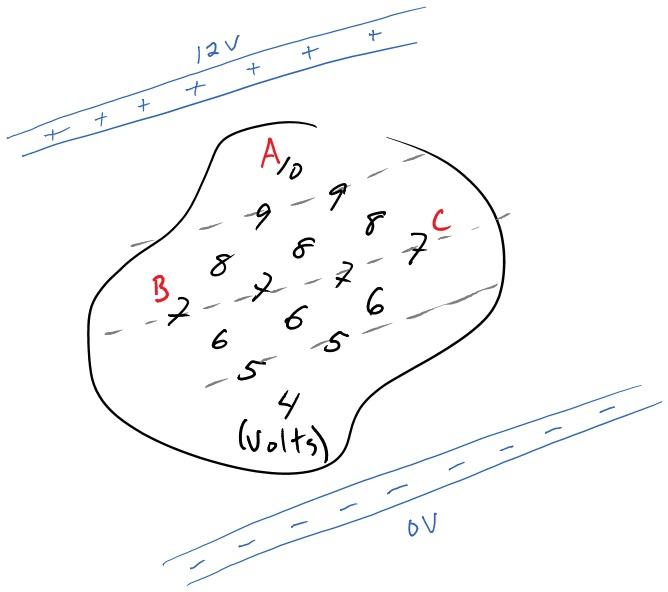
To get a better feel for how the electric potential works, lets think about fields as a map. Below is an example of an electric potential field from some group of charges that are not shown in the figure. For now don't be concerned with how the charges created this particular field, we will cover field patterns from charge distributions shortly. Instead concentrate on how the energy of a charged particle in an electric field can be analyzed. Remember that the electric potential is a scalar field and as such is just a number everywhere in space. For the electric potential it is measured in volts, the same volts you're used to with batteries and electronics. The field is there before the positive charge shown even exists.