It is easy to measure the electric potential using a volt meter. If you can map out the voltage in some region of space, you can determine the electric field from that voltage map. It is in this way that once you know the electric potential, you know everything.
Lecture 3 | Connecting Electric Potential & Electric Field
Electric Potential
Lecture 3 | Connecting Electric Potential & Electric Field
Electric Potential
Pre-lecture Study Resources
Watch the pre-lecture videos and read through the OpenStax text before doing the pre-lecture homework or attending class.
Electric Potentials | Connecting the Electric Potential and Field
Connecting the Electric Potential and the Electric Field
The electric field and potential have a close relationship. In 1-D the electric field can be thought as negative the slope of the electric potential.
$\bar{E}_x = -\frac{\Delta V}{\Delta x}$
Lessons from the above equation are:
1) if $\frac{\Delta V}{\Delta x} = constant$ (linear), then $E_x$ is constant and uniform, this is the case near large sheets of charge and in parallel plate capacitors.
2) The relationship between the electric field and potential is independent of the test charge $q_0$ - it's independent of other charges interacting with the field
3) The minus sign tells us the electric field points towards decreasing electric potential - if $\frac{\Delta V}{\Delta x}$ is negative, $E_x$ is positive
In 3-D the electric field is negative the gradient of the electric potential.
$\overrightarrow{E} = - \langle \frac{\Delta V}{\Delta x}, \frac{\Delta V}{\Delta y}, \frac{\Delta V}{\Delta z} \rangle$
A gradient is a vector and can be thought of as a kind of 3-D slope that points in the direction of steepest ascent. With the minus sign the electric field points in the direction of steepest descent. Since this is the direction of the force on a positive charge we can again make the analogous connection to the gravitational field and how water is forced to run downhill, down the direction of steepest descent. This feature adds one more lesson:
4) The electric field is perpendicular to equipotential surfaces and lines
Summary
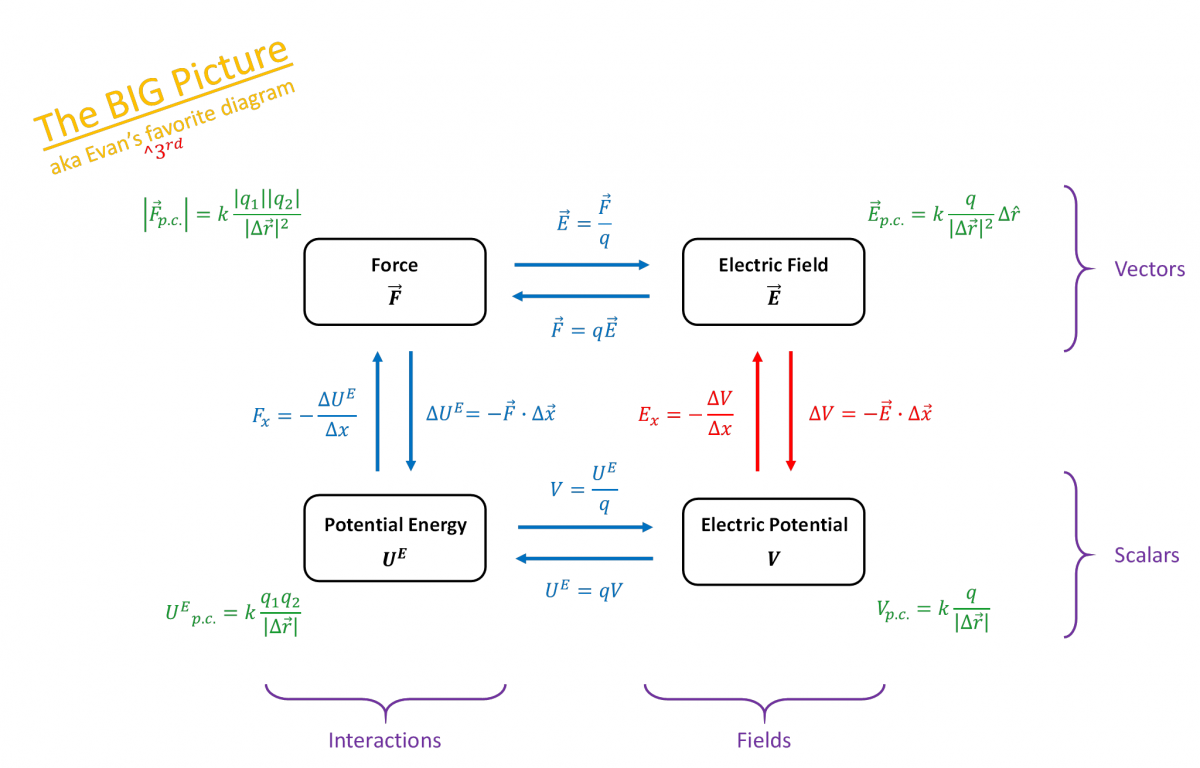
We can now go full circle with the connections between the electric field and potential, and the electric force and energy. The electric field and potential are owned by the charge distribution and preclude any interactions with new test charges $q_0$. The electric force and potential energy require an interaction with the test charge. The concept map below helps visualize the relationship.
This is an image showing how electric field, electric potential, electric force and electric potential energy are related. The electric potential in voltage is a scalar field that is related to the electric field which is a vector field by the equation electric field is equal to the negative change in voltage divided by the change in position. The electric field which is a vector field is related to the electric force which is a vector interaction by the equation electric force is equal to q naught multiplied by the electric field. The electric force which is a vector interaction is related to the electric potential energy which is a scalar interaction by the equations the negative change in electric potential energy is equal to the electric work. Another equation to show this is the electric force dot product of the change in position (but this is only true if there is a constant electric force) and this is equal to negative electric potential energy. The electric potential energy which is a scalar interaction is related to the electric potential which is a scalar field by the equations the potential electric energy is equal to q multiplied by the voltage and the change in electric potential energy is equal to q multiplied by the change in voltage.
Key Equations and Infographics
Now, take a look at the pre-lecture reading and videos below.
Required Videos
OpenStax Section 19.2 | Electric Potential in a Uniform Electric Field
Image
