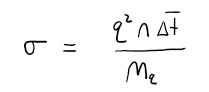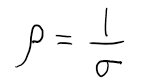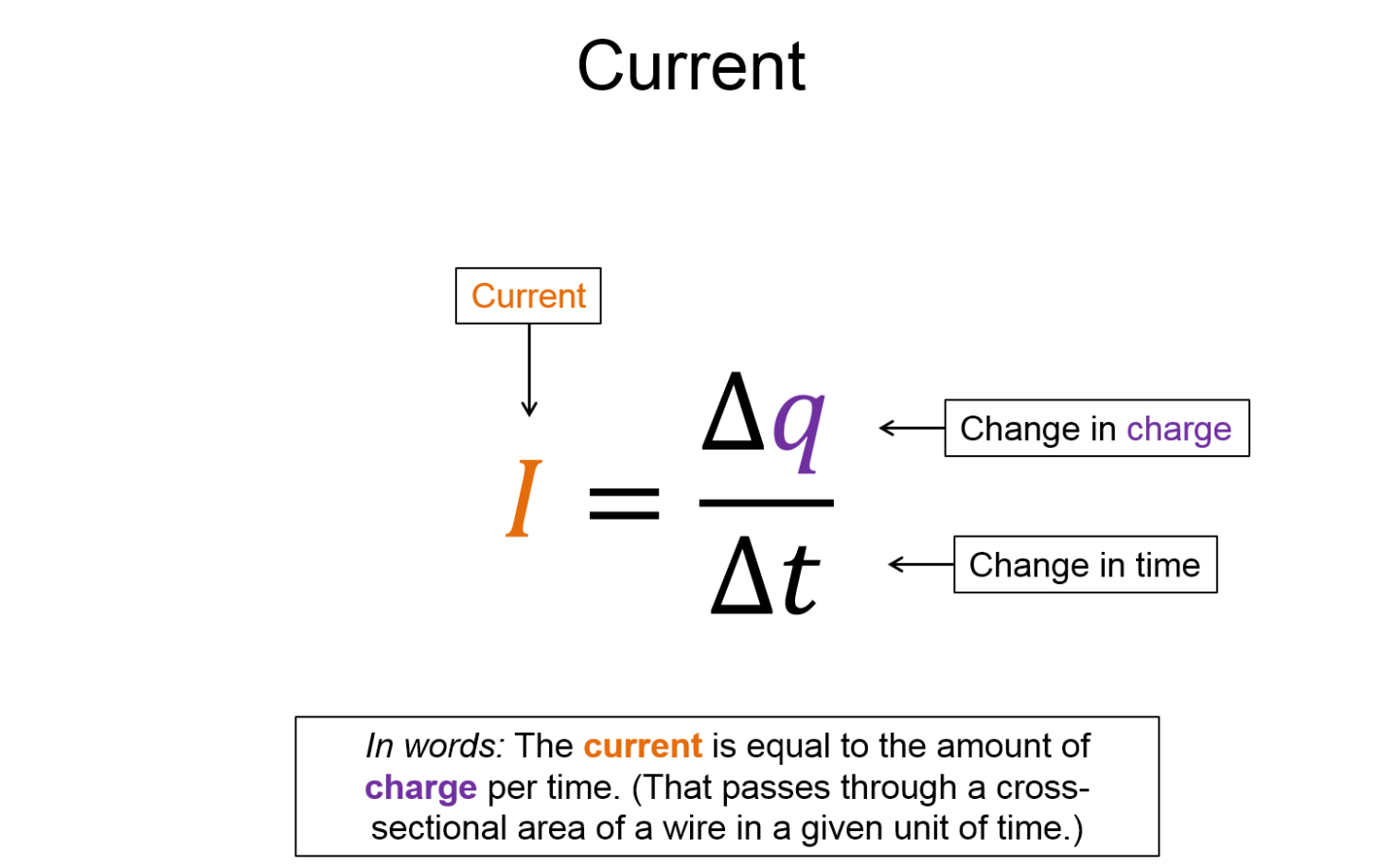Watch the pre-lecture videos and read through the OpenStax text before doing the pre-lecture homework or attending class.
Lecture 1 | Micro-model of Charge Flow, Resistance, Ohm's Law, Power
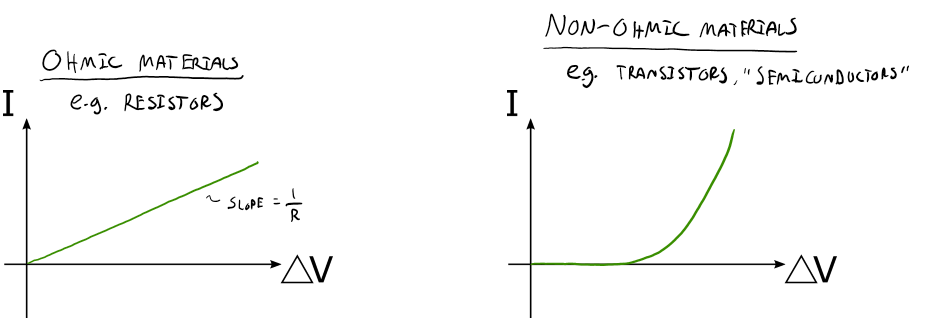
Resistive Circuits
Lecture 1 | Micro-model of Charge Flow, Resistance, Ohm's Law, Power
Resistive Circuits
Check out Crash Course Physics's introduction to electrical current.
Pre-lecture Study Resources
Resistive Circuits | Micro-model of Charge flow, Resistance, Ohm's Law, Power
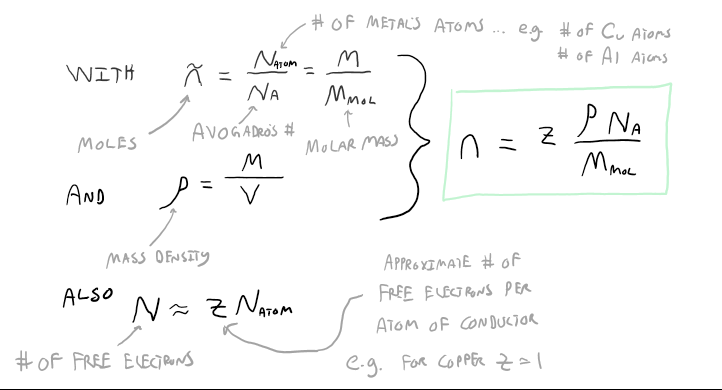
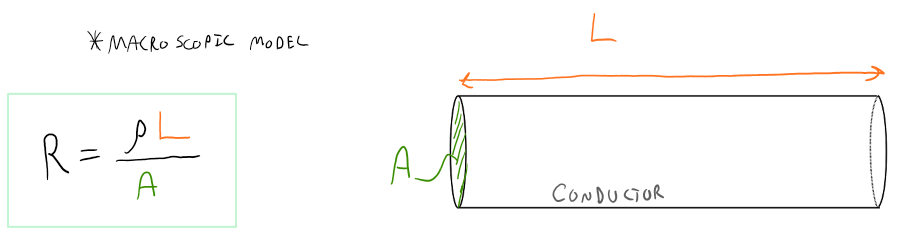
Imagine a neutral conductor, for example a thin metal rod, that is not in the presence of any external electric field. Relying on our microscopic model of matter, we can describe this metal rod as a mix of free electrons uniformly distributed throughout the volume of the rod, and tightly bound electrons in the vicinity of their corresponding positive ion cores that make up the lattice. Now imagine turning on an external electric field, for example a uniform electric field parallel to rod. Can you predict what will happen to the metal rod? Hopefully you were thinking along the lines of, "polarization". The instant the conductor finds itself inside this electric field, the free electrons feel a force due to their interaction with the electric field. This force causes the free electrons to migrate from their current location, anywhere within the rod, to the end of the rod. The migration of these electrons cannot last forever and eventually an electrostatic condition is established where one end of the rod is now more negatively charged than the other end and no more free electrons are moving towards the negative end. It turns out that the time it takes the rod to reach this electrostatic condition and become polarized happens extremely quick, on the order of microseconds or even faster. Nevertheless, we say that there is an electric current during the short time when the free electrons are moving towards the end. The electric current, or current for short, ceases to exist when the electrostatic condition is reached, after all no more free electrons would moving towards the end. In the upcoming lectures we will look at ways to establish a current that last quite a long time, seconds, minutes, hours, and even days or years. We will then study some of the applications of current, but for now this lecture will focus on developing a classical microscopic model of current. I emphasize "classical" because our microscopic model is far different than the modern quantum model. Even though a more robust model is found by invoking principles of quantum mechanics, the classical model we will develop correctly predicts common observations of the quantities related to current. Since this is an course focused on classical physics, I will drop the classical label as it is redundant. The microscopic model of current we wish to develop will draw upon much of your previous physics concepts such as: the features of conductors, electric fields, how forces and electric fields are related, how force and acceleration are related, how acceleration and velocity are related, and dimensional analysis. While constructing this microscopic model of current, we will encounter quantities that will be useful in characterizing devices that rely on current in order to perform their function (e.g. lightbulbs, speakers, car components, etc..). We will begin our development of the microscopic model of current with an electrostatics overview.
Electrostatics overview
Below is a short list of some of the features of conductors. These features will be drawn upon when constructing a microscopic model of current.
- Any net charge on a conductor resides on the surface of the conductor.
- This net charge distributes itself over the surface of the conductor such that the electric field inside the conductor is zero in electrostatic equilibrium and the electric potential (commonly referred to as voltage) is a constant within and on the surface of the conductor.
- The actual distribution of the net charge on the surface is complicated, but for highly symmetric cases the surface charge distribution is uniform (e.g. sphere or very long cylinder far away from edges).
- Example: The net charge on a very long cylinder spreads out uniformly across the surface as shown in the diagrams below. The excess charges here are considered electrons, which are represented with a negative sign ( − ). The three dimensional nature makes it challenging to illustrate a side view. Thus, only two circular strips around the surface of the cylinder are shown for simplicity. Also note that the excess electrons distribute themselves across the surface of the cylinder in such a way that the electric field inside the cylinder is zero. The ends of the cylinder are not shown because the electrons are distributed in a complicated way around the edges which isn't important for our following discussions.
- The purple numbers represent the electric potential at various locations. Notice that at this electrostatic equilibrium condition the electric potential is a constant. For example, V could be -10 volts at all locations.
Required Videos
OpenStax Section #.# | Title -- From Fundamentals
Openstax section on Electric Current covers the concepts for this section