Subject | Lecture
Basic circuit analysis - energy and power
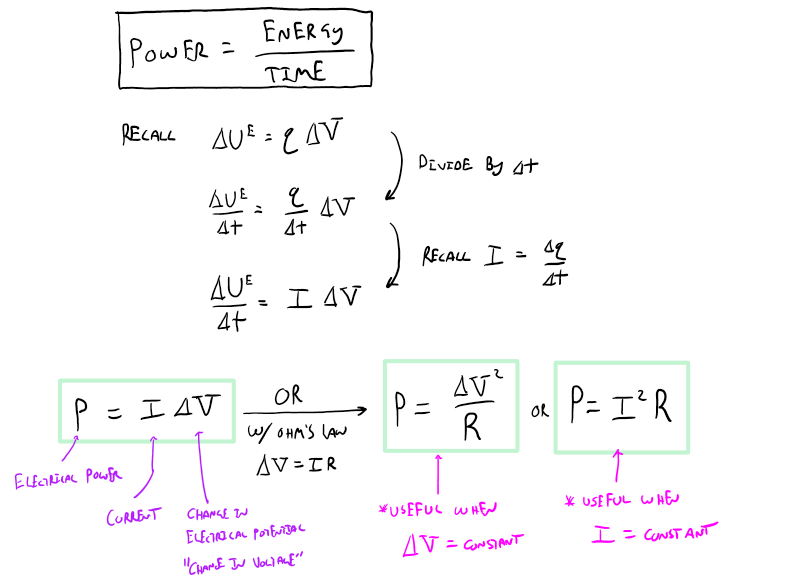
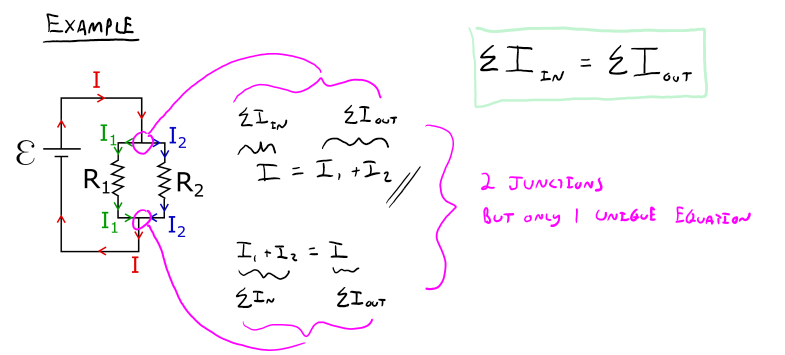
While constructing our microscopic model of charge we ran into the idea of conservation of charge. Here, conservation of charge states that the amount of charge that reaches the cross-sectional area in a given unit of time, must also leave that cross-sectional area in the same amount of time. This should make some intuitive sense, for example, if more charge enters the cross-sectional area than leaves it, then charge would build up on the cross-section. If charged built up on the cross-sectional area, then it would begin to repel the incoming charge thus reducing the current until it eventually stops. Basically, conservation of charge will ensure that our current is constant.
In this section, we will look more closely at this statement by practicing some problems that highlight how conservation of charge is used in analyzing current flowing through circuits. Before we dive into the questions, we should first define a commonly used term, junction. A junction is a location where current coming from one direction can be split into two or more directions. Luckily there is a concrete analogy we can rely on; an intersection of a road. Just like driving, if you come to a location where you have an option to go left or right, you could call that location a junction.
Batteries?
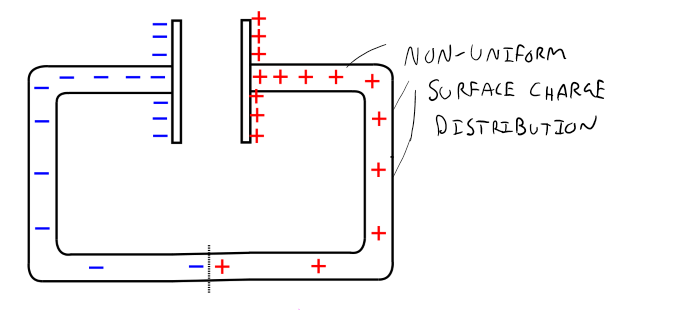
Recall that to establish a current in a wire we must create an electric field inside the wire that pushes the free electrons around inside the conductor's lattice. An equally valid statement is: to establish a current in a wire we must create an electric potential gradient (e.g. a voltage gradient) within the wire that the electrons will move up in. Remember that positive charges move down in electric potential while negative move up in electric potential. To create this electric field, or electric potential gradient, we needed to establish a non-uniform surface charge distribution along the wire. One method of creating this non-uniform surface charge distribution is to attach two places, one positive, and one negative to a wire as shown below.