Watch the pre-lecture videos and read through the OpenStax text before doing the pre-lecture homework or attending class.
Lecture 3 | Equivalent Circuits
Resistive Circuits
Lecture 3 | Equivalent Circuits
Resistive Circuits
Check out this short animation of simplifying a circuit.
Pre-lecture Study Resources
Subject | Lecture
We have previously learned how to analyze circuits using Kirchhoff's laws and Ohm's law. The method is by far the most general and will always work when trying to analyze a circuit. However, there are many different methods of analyzing circuits. In this section we will look at one such alternative method.
Some circuits have their elements connected in such a way that it is easily possible to reduce the circuit into a representative circuit consisting of only a battery and a resistor connected to each other. The ability to reduce a complicated circuit into a simpler one is often an easier way to analyze the circuit. In order to reduce a complex circuit into a simpler one, we need to first identify the two simplest ways of connecting elements and how each way can be reduced. Two of the easiest resistor combinations to reduce are known as series and parallel.
Resistors in series
When two or more elements are connected in such a way that no junctions are connected between them, then we refer to this arrangement as a series connection. The elements can be resistors, capacitors, inductors, lightbulbs etc. In this section we will only look at how resistors (and ideal lightbulbs) in series can be simplified.
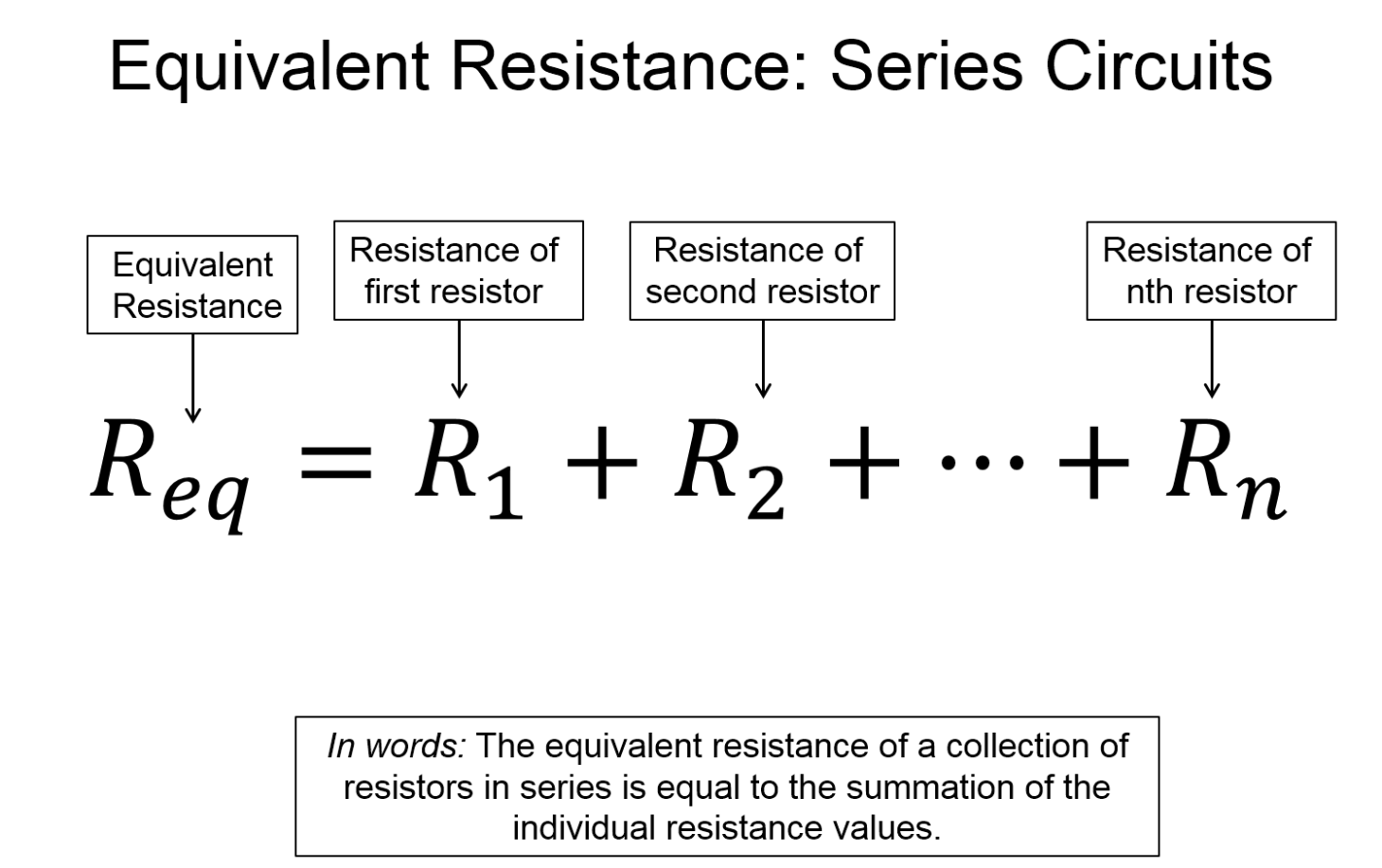
Below is a circuit diagram with two resistors in series. Using Kirchhoff's law's and Ohm's law we can create an equation, from which emerges a pattern for resistors in series. The pattern is: resistors in series can be replaced by a single resister of equivalent resistance equal to the sum of the individual resistance of each resistor that is in the series arrangement.
Two resistors in series
Note that as you add more resistors in parallel the total resistance increases, and with Ohm's law, this means that the current decreases.
Resistors in parallel
When two or more elements are connected in such a way that the change in voltage across each element is the same, then we refer to this arrangement as a parallel connection. The elements can be resistors, capacitors, inductors, lightbulbs etc. In this section we will only look at how resistors (and ideal lightbulbs) in parallel can be simplified.
Below is a circuit diagram with two resistors in parallel. Using Kirchhoff's law's and Ohm's law we can create an equation, from which emerges a pattern for resistors in parallel. The pattern is: resistors in parallel can be replaced by a single resister of equivalent resistance equal to one over the sum of the inverse of the individual resistance of each resistor that in in the parallel arrangement.
Two resistors in parallel
Note that as you add more resistors in parallel the total resistance decreases, and with Ohm's law, this means that the current increases.
The general idea for analyzing circuits with a series and/or parallel resistors is to reduce the circut to the most basic form of just one battery and one equivalent resistance. Along the way you might have to do multiple steps, for example, you may need to reduce a few reisitors in series first, then reduce more resisitors in parallel until you reach one equivalent resistance. The trick is to always draw the reduced circuit at each step. Once you reach the most reduced form of the circuit, use a combination of Ohm's law and Kirchhoff's laws as you work your way backwards through each previous reduced circuit.
Key Equations and Infographics
Equivalent Resistance: Series Circuits
Equivalent Resistance: Parallel Circuits
Now, take a look at the pre-lecture reading and videos below.
Required Videos
OpenStax Section #.# | Title -- From Fundamentals
Openstax's section on Resistors in series and parallel.
Image
