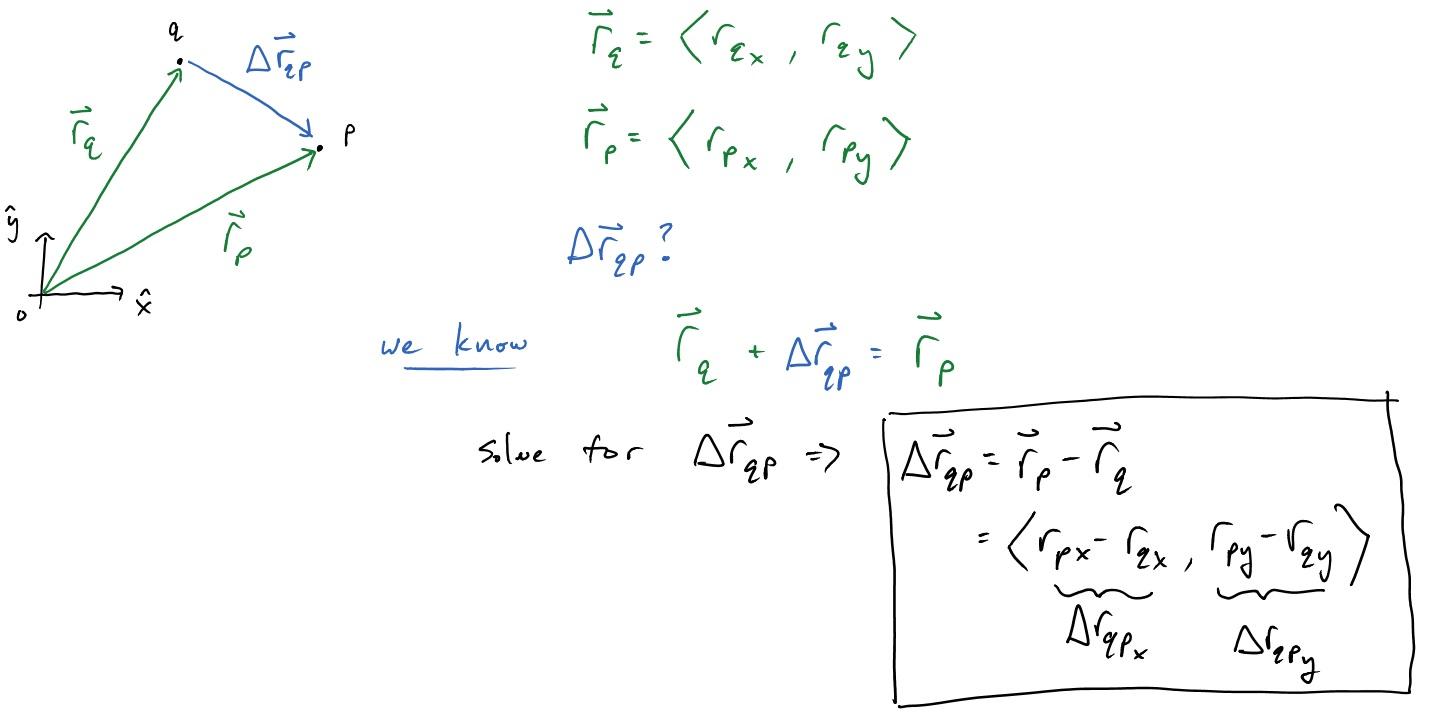Lecture 2 | Average Velocity & Acceleration

Average Quantities

Lecture 2 | Average Velocity & Acceleration

Average Quantities

Kinematics is the study of motion through describing and relating the position ($\overrightarrow{r}$), velocity $(\overrightarrow{v})$, and acceleration ($\overrightarrow{a}$) of a system. Average Quantities involves taking snapshots in time of an initial and final state of a system and finding the average of the above quantities. This section is also intended to practice vector mathematics. Operations, like adding or subtracting vectors, are a very important skill in almost all of physics, including kinematics.

The difference between speed and velocity.

The Difference Between Speed & Velocity

Pre-lecture Study Resources

Read the BoxSand Introduction and watch the pre-lecture videos before doing the pre-lecture homework or attending class. If you have time, or would like more preparation, please read the OpenStax textbook and/or try the fundamental examples provided below.

Average Quantities | Position and Displacement

You can define a position vector by it's x and y components.

$\overrightarrow{r}=\langle x, y \rangle$

You can also define the change in position (or displacement) as the final position minus the initial position.

$\Delta \overrightarrow{r}=\overrightarrow{r}_f - \overrightarrow{r}_i$

The vector diagram for a situation like this is below. In the case of position vectors, it is also what a birds-eye view might see. The axis, with origin o, defines the point <0, 0> and the positive $\hat{x}$ and positive $\hat{y}$ directions. (Note: the symbol $\hat{x}$ is called x hat and can be thought of as a way to show which direction is the positive x direction. It is technically a unit vector but that formality is unnecessary at this point.) You could imagine an object that begins at point q and after some time, ends at point p. The change in position, labeled $\Delta \overrightarrow{r}_{qp}$ points from the initial position q, to the final position p.

Displacement Vector

The first important feature of the above diagram is that the position vector $\overrightarrow{r}_q$ can be added to the change in position vector $\Delta \overrightarrow{r}_{qp}$ using the head to tail method. The vectors don't even have to be transposed because they are already setup in the correct orientation. The resultant of that addition would be the vector $\overrightarrow{r}_{p}$. The next lesson is that you can now do regular algebra on that expression and solve for any of the vectors. The change in position $\Delta \overrightarrow{r}_{qp}$ has been derived above. The expression could also have been algebraically manipulated to solve for $\overrightarrow{r}_q$ in terms of the other two. For more algebraic rules regarding vector equations, see BoxSand's pre-lecture videos.

The term Average here refers to the fact that we are only concerned with snapshots in time and the object didn't necessarily travel along the change in position vector direction. It could have followed a curved path because all we know is that it was initially in one location and is now in another. So this could be referred to as the average change in position, but we just call it the change in position.

Average Quantities | Average Velocity and Acceleration

Average velocity is just a small step away from change in position.

$\overrightarrow{v}_{average}=\frac{\Delta\overrightarrow{r}}{\Delta t}$

Here $\Delta t$ is the change in time from the initial to final position. It's important to note that when a vector quantity, such as $\overrightarrow{v}_{average}$ is set equal to another vector quantity, such as $\Delta\overrightarrow{r}$, and the only other quantity in the relationship is a scalar, such as $\frac{1}{\Delta t}$, then both vector quantities must point in the same direction. So $\overrightarrow{v}_{average}$ points the same direction as $\Delta\overrightarrow{r}$. You can also apply the same algebraic rules to this equation and solve for any of the quantities.