Lecture 1 | 1D Conservation of Momentum

Conservation of Momentum

Lecture 1 | 1D Conservation of Momentum

Conservation of Momentum

Default body text.If the impulse on a system is approximately zero, which occurs if the net force is very small or the duration of the force is very small, then the change in momentum is also approximately zero. That means that if you vectorially add up all the momentum in your system initially, it will equal the net momentum of the system finally. Mathematically this can be written as $\sum{\vec{p}_i} = \sum{\vec{p}_f}$. Applying momentum conservation when applicable will allow you to determine the motion of systems before and after collisions and other interesting scenarios.

Check out this trailer from OpenStax about collisions.

Pre-lecture Study Resources

Read the BoxSand Introduction and watch the pre-lecture videos before doing the pre-lecture homework or attending class. If you have time, or would like more preparation, please read the OpenStax textbook and/or try the fundamental examples provided below.

Momentum | Conservation of Momentum

The impulse momentum theorem states that the change in momentum on a system is equal to the average net force multiplied by the change in time.

$\Delta{}\vec{p} = \Sigma{}\overline{\vec{F}}_{external}\Delta t$

If the right-hand-side of this equation is zero or approximately zero, than the left-hand-side must also be very small. When this condition is met, the change in momentum of a system is zero. This often is the case when collisions occur if you include the objects colliding into your system. If you consider two billiard balls colliding, individually they have the force from the other billiard ball acting on them, which in turn changes their momentum during the collision. If you include both balls in your system though, and draw a dotted line around both, then the force between them becomes an internal force and the net external force is very small during the collision. The normal force from the table cancels out the gravitational force. The force from friction on the table may be considered a net external force while the balls interact but this happens so quickly that $Delta t$ is very small. Thus the impulse acting on the system is approximately zero and the net momentum does not change. This can mathematically be applied with the following.

if $\Sigma{}\overline{\vec{F}}_{external} \Delta t \approx 0$, then $\sum{\vec{p}_i} = \sum{\vec{p}_f}$

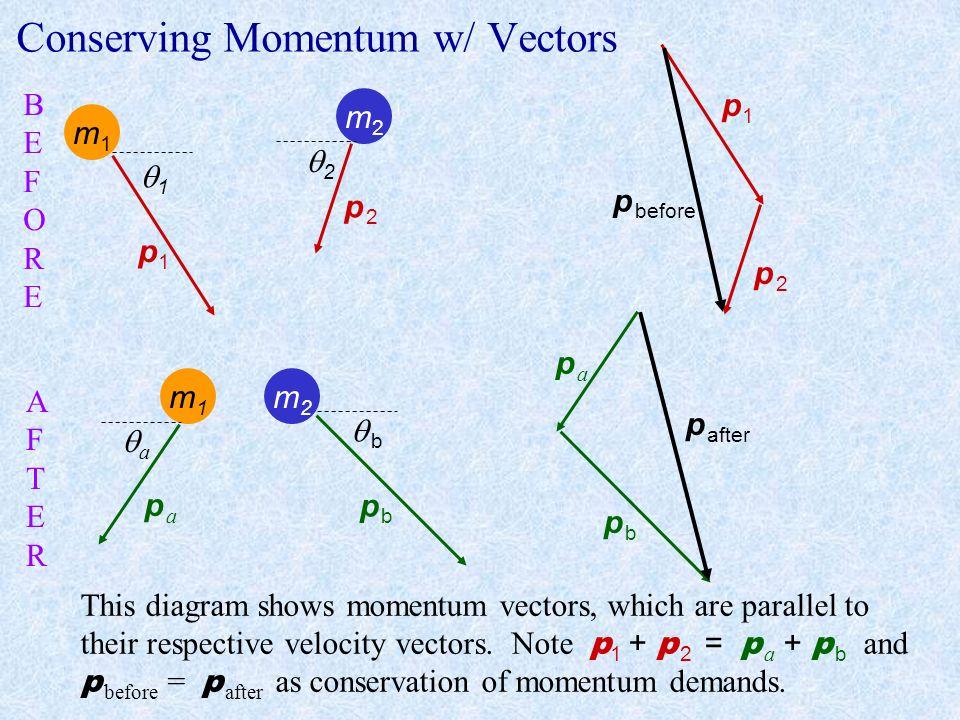
The appropriate physical representation to analyze the interaction is a vector operation of addition of momentum, like that shown below.

Conservation of momentum with vectors

Remember momentum is a vector quantity, so $\sum{\vec{p}_i} = \sum{\vec{p}_f}$ implies more than one equation, in principle it is three equations, one for each direction or component of momentum. The first equation says add up all the initial x-components of the momentum for every object and set that equal to the summation of all the final momentums in the x-direction. Then the same for the y and z-component of the net momentum.

$\sum{{p_i}_x} = \sum{{p_f}_x}$

$\sum{{p_i}_y} = \sum{{p_f}_y}$

$\sum{{p_i}_z} = \sum{{p_f}_z}$