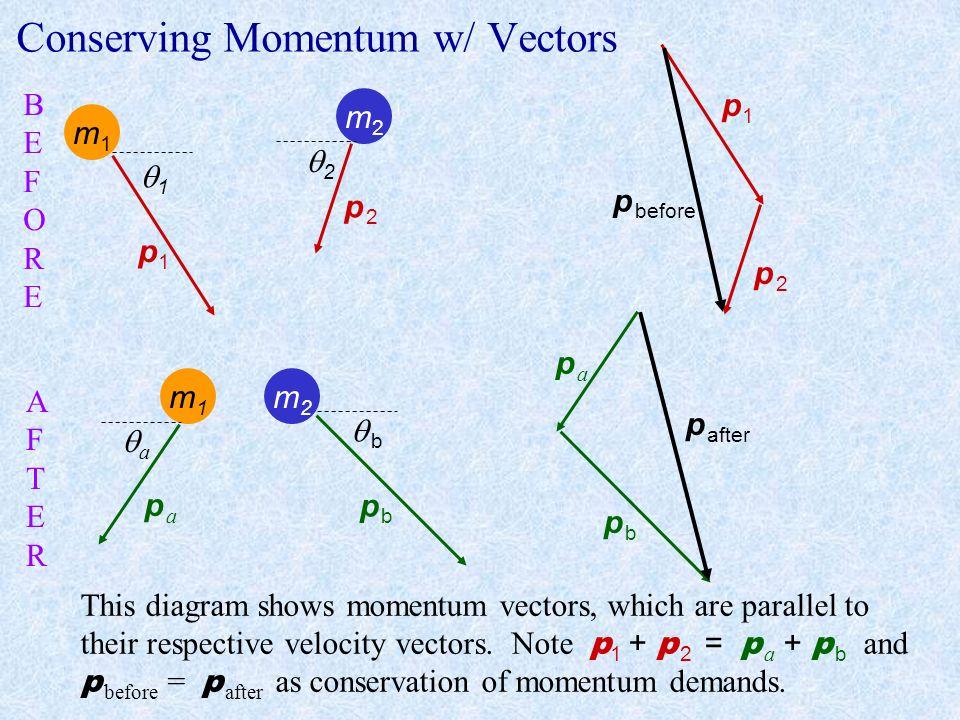
Conservation of Momentum in 2 dimensions follows the same fundamental equations and principles as in 1 dimension. The main difference is that you must use a component analysis and conserve momentum in in both x and y directions.
Check out the Space Blog for a primer on the subject.
Read the BoxSand Introduction and watch the pre-lecture videos before doing the pre-lecture homework or attending class. If you have time, or would like more preparation, please read the OpenStax textbook and/or try the fundamental examples provided below.
The impulse momentum theorem states that the change in momentum on a system is equal to the average net force multiplied by the change in time.
$\Delta{}\vec{p} = \Sigma{}\overline{\vec{F}}_{external}\Delta t$
If the right-hand-side of this equation is zero or approximately zero, than the left-hand-side must also be very small. When this condition is met, the change in momentum of a system is zero. This often is the case when collisions occur if you include the objects colliding into your system. If you consider two billiard balls colliding, individually they have the force from the other billiard ball acting on them, which in turn changes their momentum during the collision. If you include both balls in your system though, and draw a dotted line around both, then the force between them becomes an internal force and the net external force is very small during the collision. The normal force from the table cancels out the gravitational force. The force from friction on the table may be considered a net external force while the balls interact but this happens so quickly that $Delta t$ is very small. Thus the impulse acting on the system is approximately zero and the net momentum does not change. This can mathematically be applied with the following.
if $\Sigma{}\overline{\vec{F}}_{external} \Delta t \approx 0$, then $\sum{\vec{p}_i} = \sum{\vec{p}_f}$
The appropriate physical representation to analyze the interaction is a vector operation of addition of momentum, like that shown below.
This is a representation of conserving momentum with vectors. It shows a two snapshots of before and after they collide. In the before snapshot, two balls with different masses denoted as m one and m two where both balls are moving down and towards each other with some momentum at some angle theta one and theta two. In the after snapshot, the two balls are moving down and away from each other at a new and different momentum denoted as momentum a for mass one and momentum b for mass two at new angles theta a and theta b respectively. There are two triangles that shows the change in momentum before and after the collision of the two masses. It is noted below that this diagram shows momentum vectors, which are parallel to their respective velocity vectors. Note momentum one plus momentum two is equal to momentum a plus momentum b and the change in momentum before is equal to the change in momentum after as conservation of momentum demands.
Remember momentum is a vector quantity, so $\sum{\vec{p}_i} = \sum{\vec{p}_f}$ implies more than one equation, in principle it is three equations, one for each direction or component of momentum.
$\sum{{p_i}_x} = \sum{{p_f}_x}$
$\sum{{p_i}_y} = \sum{{p_f}_y}$
$\sum{{p_i}_z} = \sum{{p_f}_z}$
Openstax Section 8.6 | Collisions of Point Masses in Two Dimensions
