Lecture 1 | Angular Momentum & Rotational Energy

Rotation & Conserved Quantities

Lecture 1 | Angular Momentum & Rotational Energy

Rotation & Conserved Quantities

Angular momentum helps us think about how difficult it would be to stop something from spinning if the rotational speed of the object and it's distribution of mass around the axis of rotation was varied. Stopping a merry-go-round is much harder when its full of children. Angular momentum is often used when talking about extended masses, such wheels rotating about an axle or ice skaters spinning faster and faster. Specifically it tells you how hard it is to stop a rapidly spinning object in a certain amount of time, much like linear momentum tells you how hard it is to stop something moving translationally in a given amount of time. It is a useful property for understanding the orbits of satellites and planets. Like linear momentum, angular momentum is conserved for isolated systems. Physics assumes the angular momentum of the universe is a constant!

Here is a quick concept trailer of angular momentum from OpenStax

Pre-lecture Study Resources

Watch the pre-lecture videos and read through the OpenStax text before doing the pre-lecture homework or attending class.

Rotation and Conserved Quantities | Angular Momentum and Rotational Kinetic Energy

Angular Momentum

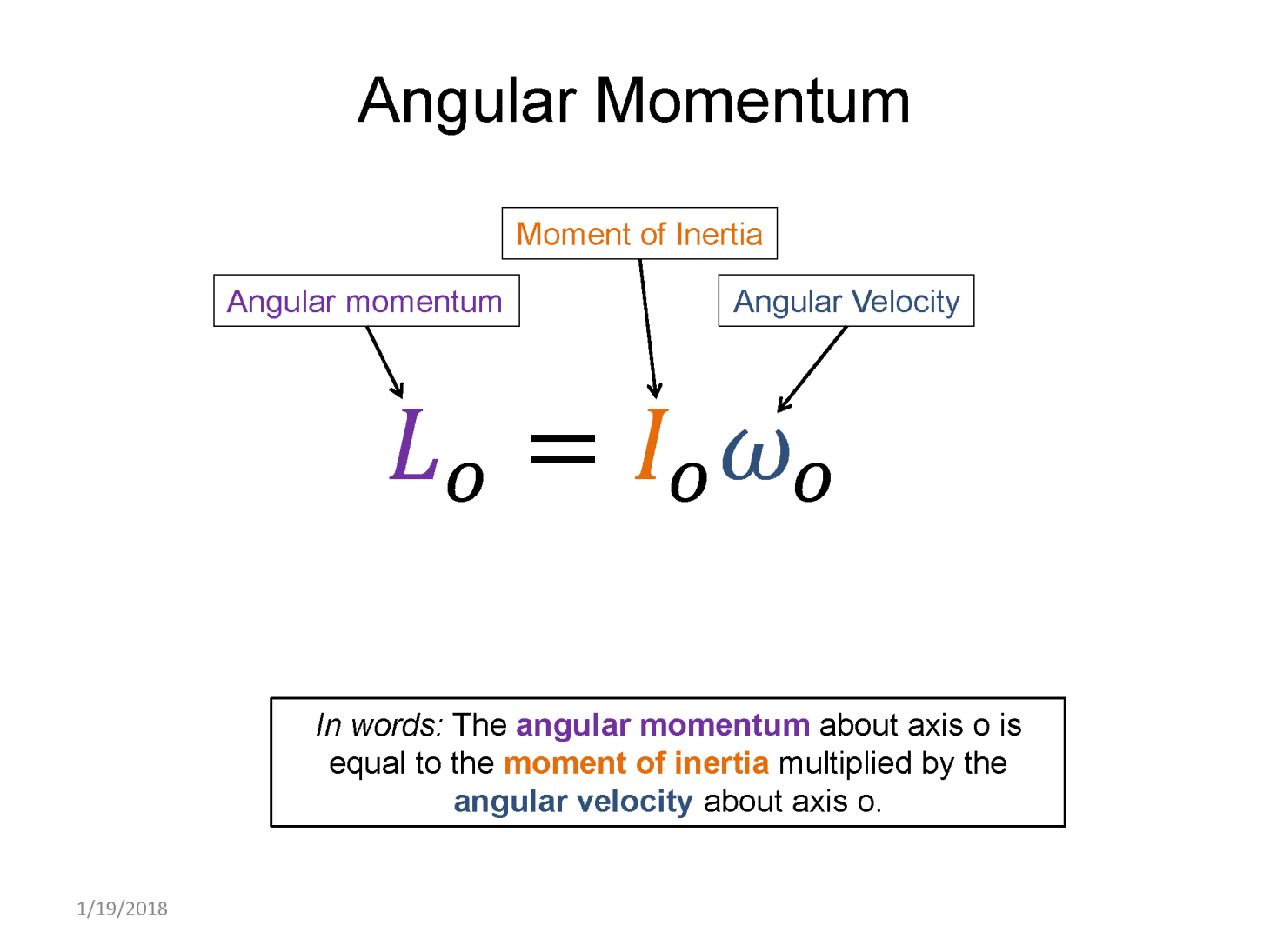
Just as linear momentum represents a quantity that scales a mass by its velocity, angular momentum represents a quantity that scales the extended mass of an object by its angular velocity. It is mathematically defined as

$ L = I \omega$

where $I$ is the moment of inertia of an object, and $\omega$ is its angular velocity. Angular velocity is a vector quantity but we will not be discussing that aspect and instead will use a sign convention that it can take positive or negative values: (+) for counter-clockwise motion or (-) for clockwise motion. Angular momentum is helpful for understanding the motion of real-life objects, such as rotations of galaxies about their galactic center or the motion of a merry-go-round as a child walks from the outside in.

If we compare the linear and angular momentum equations directly we see they are very similar:

$p = m v $

$L = I\omega$

Where the moment of inertia, which represents how the mass is distributed about some point, takes the place of mass; and omega, which represents how that extended mass is moving about a point, takes the place of velocity.

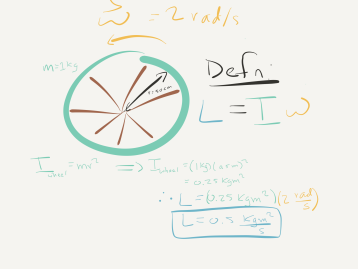
As a quick example, imagine a wheel with a mass of 1kg and a 50 cm-diameter spinning about an axle at a rate of 2 rad/sec. If we assume the spokes are massless we can use the moment of inertia for a spinning ring, $I_{ring} = mr^2$, to describe the wheel, where $r$ is the radius of the wheel and $m$ is the mass of the wheel:

above is the sort of calculation you will do a lot of in this section.

Just like linear momentum, angular momentum is a conserved quantity with its own conservation law:

$\Sigma \tau_{ext} \Delta t = \Delta L$

This equation says that if the net external torque is zero, angular momentum will not change. This equation is just like the impulse-momentum theorem from linear momentum and, when we plot $\Sigma \tau_{ext}$ (also known as $\tau_{net}$) versus $\Delta t$, we can find the area under the curve to determine how much angular momentum has changed in some time interval. This is exactly the same as how we used plots of $F_{external}$ versus $\Delta t$ to determine how much linear momentum would change in some time interval!

For example, imagine you're riding an electric scooter. The electric motor in the scooter applies a torque to the wheels to get them to spin. We can determine how much angular momentum is being added to the wheel by examining the torque versus time plot:

And since we know $\Delta L = \Delta (I\omega)$, and we know $I$ isn't changing (the diameter of the wheels on your scooter isn't changing) we can find the change in angular velocity:

$ I_{wheel} \Delta \omega = \Delta L$ and $\Delta L = \tau_{motor} \Delta t$

→$\Delta \omega_{wheel} = \frac{\tau_{motor} \Delta t}{I_{wheel}}$

In general, to find a value for "tau times delta t" in the numerator of the right-hand-side, you will make triangles and squares out of the area under the curve; often (as in this example) the "tau versus delta t" looks like $\frac{1}{2}bh$ where $b$ is the base length ($\Delta t$) and $h$ is the height ($\tau_{max}$), which reduces to $\frac{1}{2}{\tau_{max}}\Delta t$

Rotational Kinetic Energy

Rotational kinetic energy accounts for the collective motional energy of mass(es) rotating about an axis. Imagine a bowling ball sliding on a frictionless surface with some speed v. It would have linear kinetic energy ($\frac{1}{2}mv^2$) from the translational motion of all the particles making up the ball. If the ball was instead rolling, but yet it's center of mass still had a speed v, there would be additional motional energy in the rotation of all the particles that make up the ball about the axis of rotation. Rotational kinetic energy ($\frac{1}{2}I\omega^2$), where I represents the moment of inertia about the rotational axis and $\omega$ represents the angular velocity about the axis of rotation, accounts for this additional motional energy.

$K_{total}=K_{linear}+K_{rotational}$

$K_{total}=\frac{1}{2}mv^2+\frac{1}{2}I\omega^2$

After accounting for this new form of rotational kinetic energy, the rest of a standard energy analysis follows. Add up all the initial total mechanical energy (E), kinetic (K) plus potential (U), then add the work from non-conservative forces, and set that equal to the final mechanical energy.

$\sum E_i + W_{nc} = \sum E_f$, where $E = K_{linear} + K_{rotational} + U$