Check out the Original Double Slit Experiment
Breadcrumb
- BoxSand
- Optics
- Back to Wave Optics
- Lecture 1 | Young's Double Slit
Lecture 1 | Young's Double Slit
Wave Optics
Lecture 1 | Young's Double Slit
Wave Optics
The Original Double Slit Experiment
Pre-lecture Study Resources
Watch the pre-lecture videos and read through the OpenStax text before doing the pre-lecture homework or attending class.
Wave Optics | Young's Double Slit Experiment
Superposition of Waves
When two waves enter the same region of space at the same time they interfere in a way that obeys the Superposition of Waves. This addition of waves creates places where the peaks line up and the resultant wave is larger, which would manifest as a bright spot for light waves. There are also regions where the peak from one wave is lined up with the trough from the other and the resultant is wave cancelation, where their amplitudes add to zero and there would be a dark spot. These constructive and destructive areas are seperated by an entire gradient of partially constructive and partially destructive. The resulting interference pattern is one of the defining features of a wave
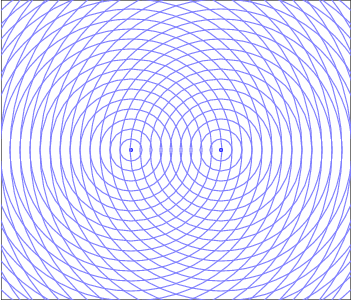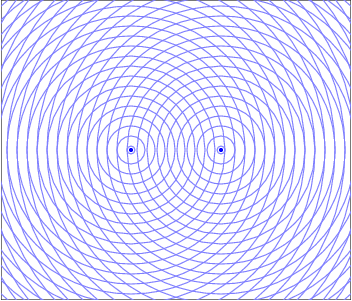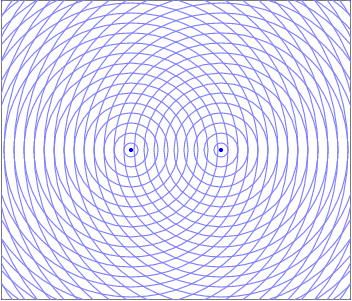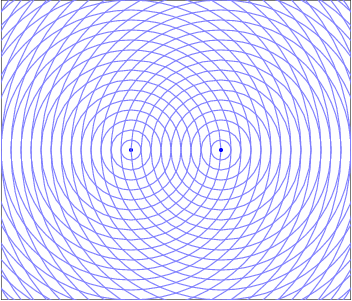
An animated image depicting Two Source Interference. Two point sources are spaced a short distance apart and are emitting circular waves represented by successive circles, each of which grow larger as time passes. Where the circles overlap, wave crests add constructively. Where a gap between circles from one source overlaps with a circle from another source, destructive interference results. There is a spatial interference pattern that is visible around the two sources, with alternating lines of constructive and destructive interference radiating away from the two point sources at the center of the pattern.
Wave Interpretation of Light - Young's Double Slit Interference
The theory of Electromagnetic Radiation Wave Theory is one of the most tested and confirmed theories in physics. It relies heavily on the experimental fact that light has wave-like properties. These wave-like properties are displayed by the interference effects that has only been observed in wave systems. The hallmark experiment that enabled us to observe the effect was Young's Double Slit Experiment.
To observe the interference of two sources you need two, coherent, single frequency sources. Essentially you would like two identical sources. The clever way Young achieved this was by isolating a single color of light then sending that light through two small slits. Each slit acts like a new wave source due to the diffraction of light, which is the effect that light "bends" around corners and spreads out when passing through an opening. Since each slit acts like a new source, and each originated from the same source, they are two coherent, single frequency (same color) sources. The diagram below shows a snapshot of the waves as they interfere.

The image illustrates a diagram of the double-slit experiment. On the left is a light bulb labeled "Light," emitting waves that pass through a "Single Slit." These waves then encounter a "Double Slit" in the middle of the image, where they split into multiple waves, creating an overlapping pattern. This results in an "Inference Pattern" displayed on the right side on a "Screen." The pattern on the screen shows alternating dark and light bands, demonstrating the wave interference.
The modern technology of a LASER (Light Amplification through the Stimulation of Electromagnetic Radiation) has made this experiment much easier due to the very high intensity soures they provide. The experiment also enables one to measure the wavelength of visable light, something on the order of hundreds of nanometers, a size only an order of magnitude greater than the size of atoms. For nearly 100 years this was the only way to probe scales this size scale and it still remains as one of the best.
The geometry of Young's Double Slit is below.

A diagram showing the interference pattern produced by double slits. A plane wave passes through two slits, producing two waves with amplitudes that are in phase. The separation between slits in the screen is given the symbol, d. The light passing through the slits shines on a screen, a distance D away, forming a spatial interference pattern of bright and dark bands of light.
Light passing through each slit shines in all directions. A line is drawn from each slit. The two lines meet at the same point on the screen. If the distance to the screen, D, is much larger than the slit separation, d, then these two lines are roughly parallel. The angle these lines make with the optical axis is labeled theta.
A triangle is drawn to show that the extra distance traveled by one of the waves along these lines is found using trigonometry to be delta = d multiplied by the sine of theta. Another triangle is drawn to show that the tangent of the angle theta is the distance, y, from the optical axis to a bright band divided by the distance between the slits and the screen, D.
A red sinusoidal pattern is drawn on the screen to illustrate the intensity of the light. The location on the screen directly opposite the two slits is a maximum in intensity.
Two additional equations used to analyze double slit interference are written.
Here the dstance between the slits is $d$ and the screen observing the interference effect is a distance $D$ away from the slits. The central maximum is located along the perpendicular bisector between the two sources where the Path Length Difference (PLD) between the two sources is zero. The condition for constructive interference is for the PLD to be an interger ($m$) multiple of the wavelength. So as you move away from the central maximum and go from constructive to destructive and back to constructive, you've increased the PLD by one whole wavelength. These bright spots are called interference fringes. Using the condition for constructive interference $PLD = m \lambda$ and the geometry that $PLD=d sin(\theta)$, you arrive at the overall condition for constructive interference.
$d sin{\theta}=m \lambda$
The distance $y$ is measured from the central maximum and can be related to the angle ($\theta$) and the distance $D$ by the equation $tan (\theta) = \frac{y}{D}$. In most cases, where $\lambda << d$ the angle is so small that $sin (\theta) \approx \theta$. Since $tan (\theta) = \frac{sin(\theta)}{\cos(\theta)}$ and $\cos(\theta) \approx 1$ for very small angles, $tan(\theta) \approx sin(\theta) \approx \theta$. This allows a more simple connection between the variables shown in the equation below, but note, this only if the angles are very small.
$y \approx \frac{m \lambda D}{d}$, if $\lambda << d$
Key Equations and Infographics





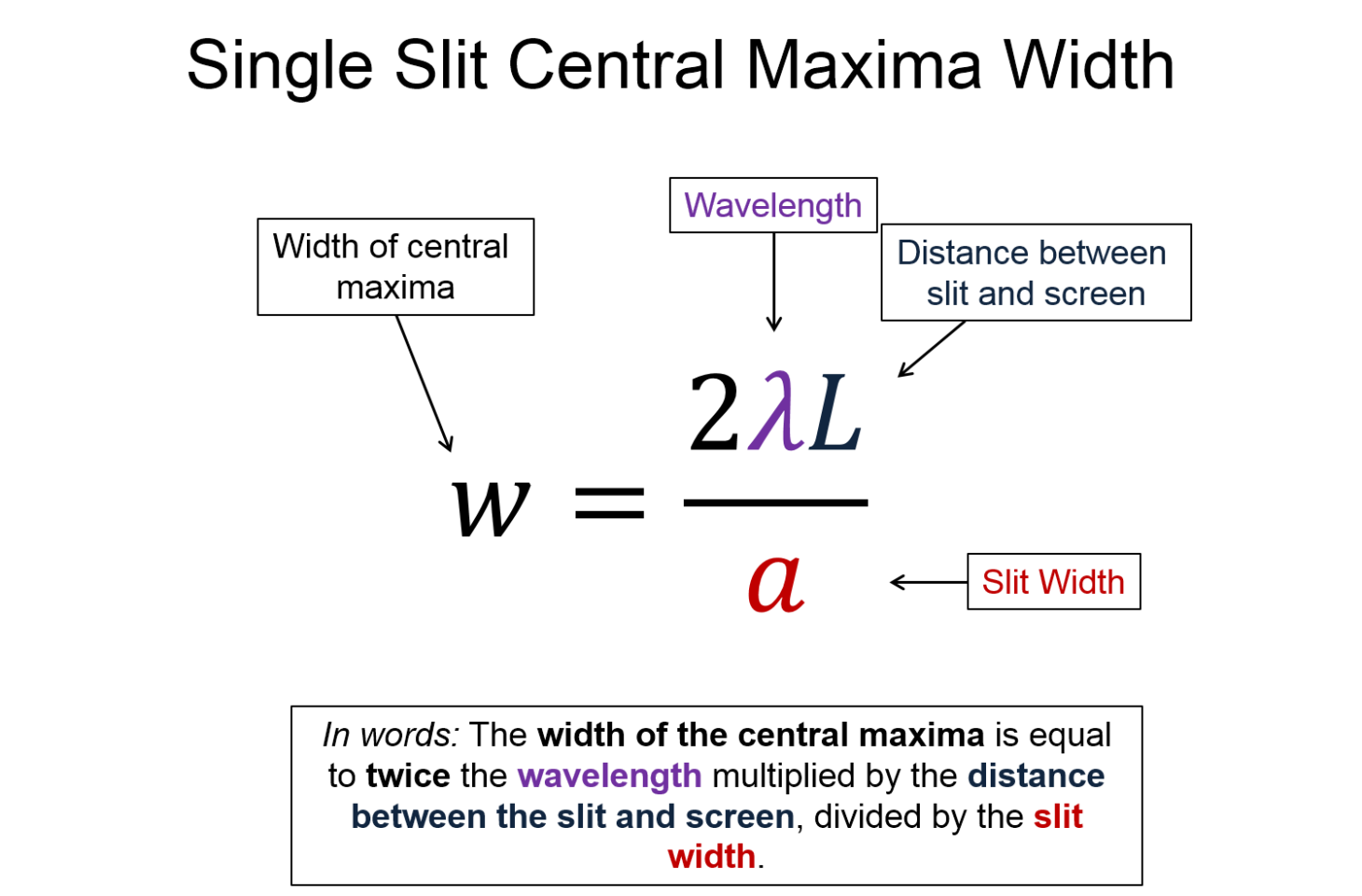
Now, take a look at the pre-lecture reading and videos below.
Required Videos
ph203 - s2014 - Youngs Double Slit - Apparatus and conceptual (15min)
ph203 - s2014 - Youngs Double Slit - Apparatus and conceptual review(2min)
ph203 - s2014 - Youngs Double Slit - governing equations (6min)
Suggested Supplemental Videos
ph203 - s2014 - Youngs Double Slit - example - simple with small angle (5min)
ph202_Superposition - Two source Interference - example - sound double slit(10min)