Lecture 1 | General Oscillations, Simple Harmonic Motion, Equations of Motion

Oscillating Systems

Lecture 1 | General Oscillations, Simple Harmonic Motion, Equations of Motion

Oscillating Systems

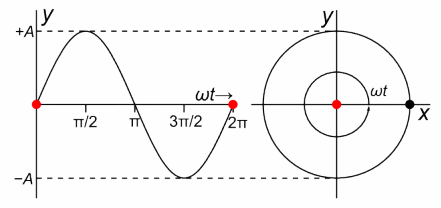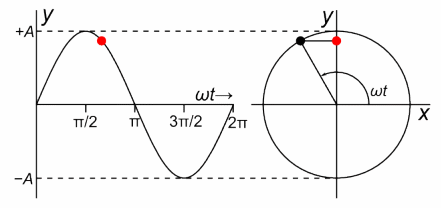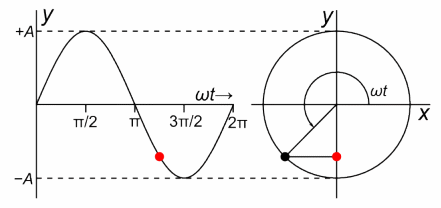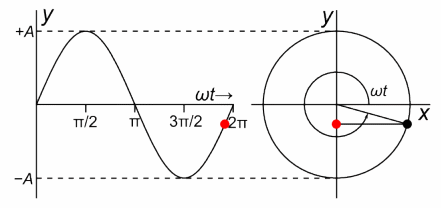
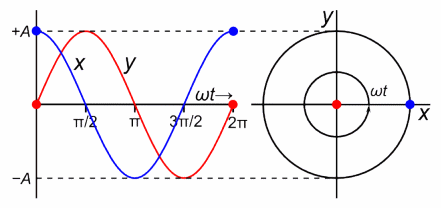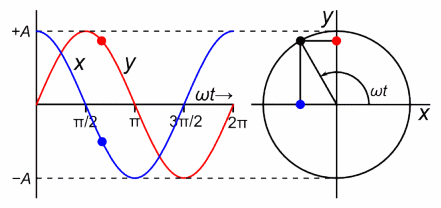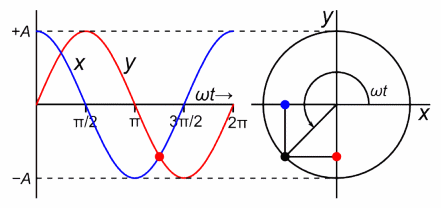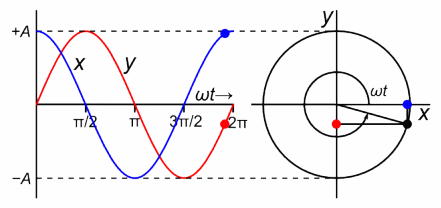
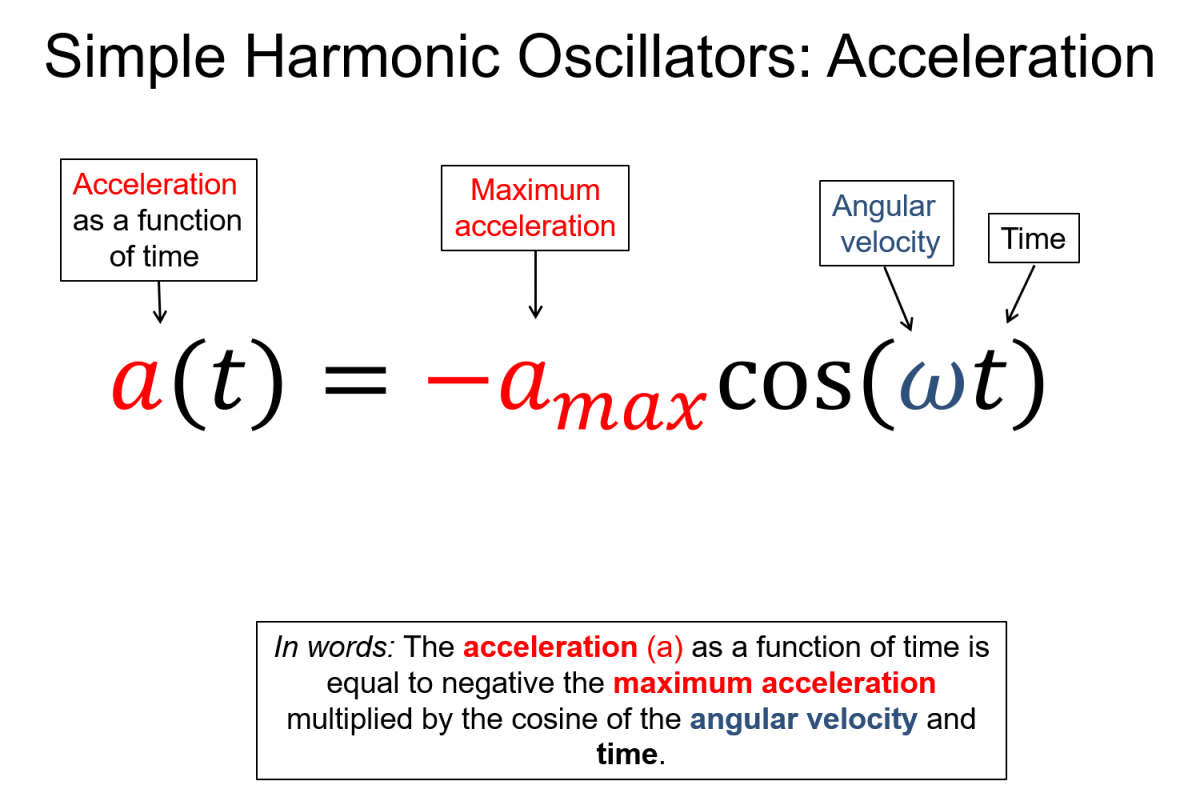
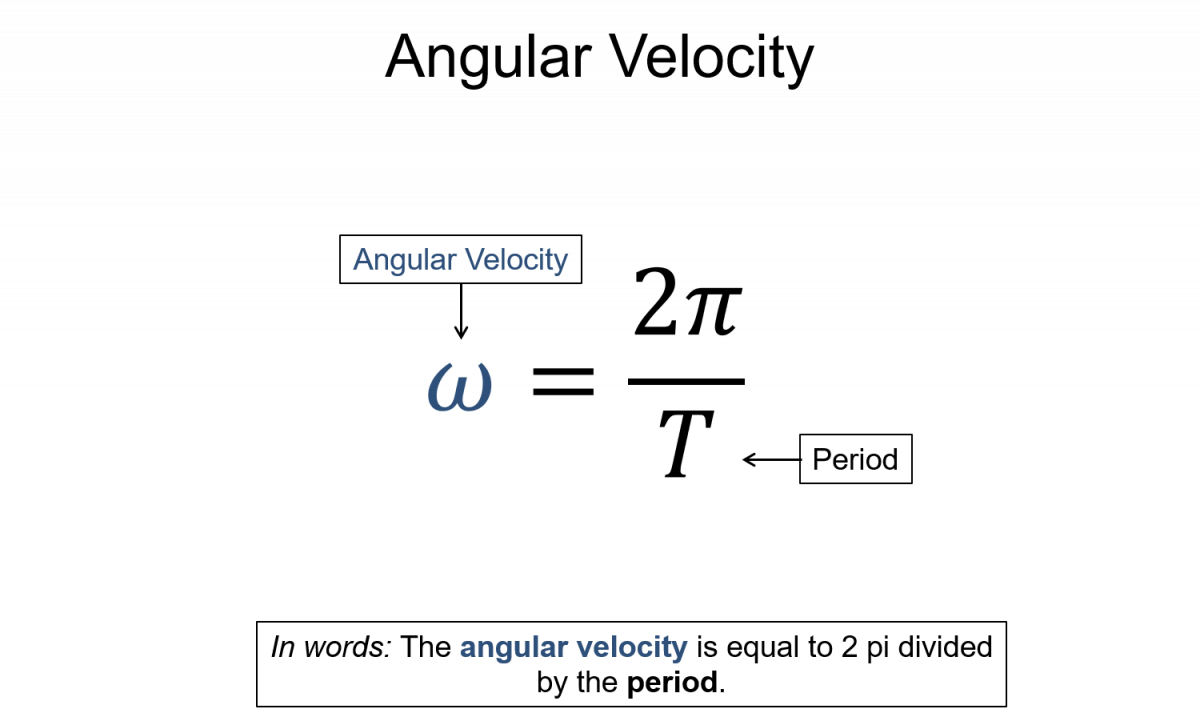Oscillations are one of the most prevalent phenomena in our universe. From a swinging tree branch, to molecular vibrations, even to the orbits of celestial bodies, repetitive events happen everywhere in nature. Simple harmonic oscillators (SHO) are specific type of oscillation where the motion can be described by sinusoidal functions and the time per revolution (period) is independent of the amplitude of the vibration.

Pre-lecture Study Resources

Watch the pre-lecture videos and read through the OpenStax text before doing the pre-lecture homework or attending class.

Oscillations occur all around you - anything that repeats could be considered an oscillation. There are obvious macroscopic oscillations, such as a mass connected to a spring (shocks on car) or a simple pendulum (grandfather clock), but oscillations are actually pervasive at all scales. The binding between two molecules acts very similar to if you had connected those molecules by a tiny spring. All matter is vibrating, and solids vibrate like little masses connected by little springs. The greater the temperature, the greater the energy and amplitude of the vibrations - the molecules wiggle more. On the celestial scale the moon orbits the Earth, which in turn orbits the sun. Then the whole solar system orbits the black hole at the center of our galaxy. Theorists and philosophers have even predicted The Big Bang is followed by a Big Crunch that is then followed by another big bang and the whole process repeats - this viewpoint is not in particular favor these days but give it more time and it may come back, kind of like an oscillation.

--Forces and Energy--

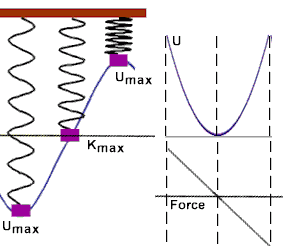
All classic oscillations have a few things in common. First, when the system is displaced from its current state, there is a Restoring Force that drives it back. Think of a spring stretched or compressed, it has a spring force driving it back towards its relaxed length. Second, the potential energy (PE) function (U) of the system must have a Potential Energy Well. A PE well is a point where the potential energy increases in all directions. There are local and global wells, which refer the size scale in question. For example, water in my cup on my desk is in a local gravitational PE well but if it splashes out it could fall completely off the desk onto the floor, which may be considered a more global well. If you recall for a spring the potential energy is $\frac{1}{2}k \Delta x^2$, which is a quadratic function centered around $\Delta x = 0$. This is a potential energy well that increases for both positive and negative values of $\Delta x$, as shown below.

All oscillators share in common a restoring force and a potential energy well. What differentiates harmonic oscillators from other, non-harmonic oscillators, is the functional form of these forces and potential energy functions. A system will undergo simple harmonic motion if the restoring force is linearly dependent on the displacement from equilibrium.

$Force \propto x$

This means if the displacement is doubled, than so is the restoring force. A system will also undergo simple harmonic motion if the potential energy function that arises from the restoring force is quadratic with respect to displacement from equilibrium.

$Potential Energy \propto x^2$

This means that if the displacement doubles, the potential energy increases by a factor of four. These two features are actually dependent on each other and if the restoring force is linear, then the PE is quadratic (and visa versa).

Another important feature of a simple harmonic oscillator is that the period of the motion is independent of the energy. Consider a spring with a mass oscillating. As the system loses energy and the amplitude of the oscillation decreases but the time it takes for one cycle will remain constant.

--Position, Velocity, Acceleration--

All oscillators display repetitious behavior in their kinematic equations (position, velocity, and acceleration), but Simple Harmonic Oscillators display distinctively sinusoidal behavior.

The exact form of the sinusodial equation depends on what are called the initial conditions, which is the state of the system at time equals zero. At t = 0 in the plots above, the system's position is a positive maximum, the velocity is zero, and the acceleration is at a negative maximum. If you were to hang a mass from a spring and release it from rest from its maximum height (assumed up is positive direction), it would ocsilate about and equilibrium position and could be described by the functions above (assuming no energy loss).

--Omega and Uniform Circular Motion--

The omega found in the above equations is the same one used for angular velocity in Uniform Circular Motion (UCM). It's related to the period is the same way as well.

$\omega = \frac{2\pi}{T}$, where T = period

To see the connection, the animation below shows the projection on the y-axis of an object in UCM. It takes the same amount of time for a complete oscillation and thus they each have the same $\omega$.