We dedicated a section with the title Heat to cover the concepts of a material property called Specific Heat and Latent Heat of Transformation, along with the experimental tool called Calorimetry. Specific heat is a measure of how much energy (per mass) must be exchanged to change the temperature of a substance a certain amount. Latent heat of transformation is a measure of how much energy (per mass) must be exchanged to take a substance over a phase transition, like from a liquid to a solid. Calorimetry is a technique to put different substances together in an isolated (no exchange of energy with the environment) container, and use their transfer of energies between each other, to determine the final equilibrium temperature of the system or to measure specific heats of one of the substances.
Lecture 2 | Specific Heat, Phase Transformations, Calorimetry
1st Law & Heat
Lecture 2 | Specific Heat, Phase Transformations, Calorimetry
1st Law & Heat
Pre-lecture Study Resources
Watch the pre-lecture videos and read through the OpenStax text before doing the pre-lecture homework or attending class.
Thermo | Specific Heat, Phase Transformations, Calorimetry
The section is dedicated to Specific Heat, Latent Heat of Transformation, and the experimental technique of Calorimetry.
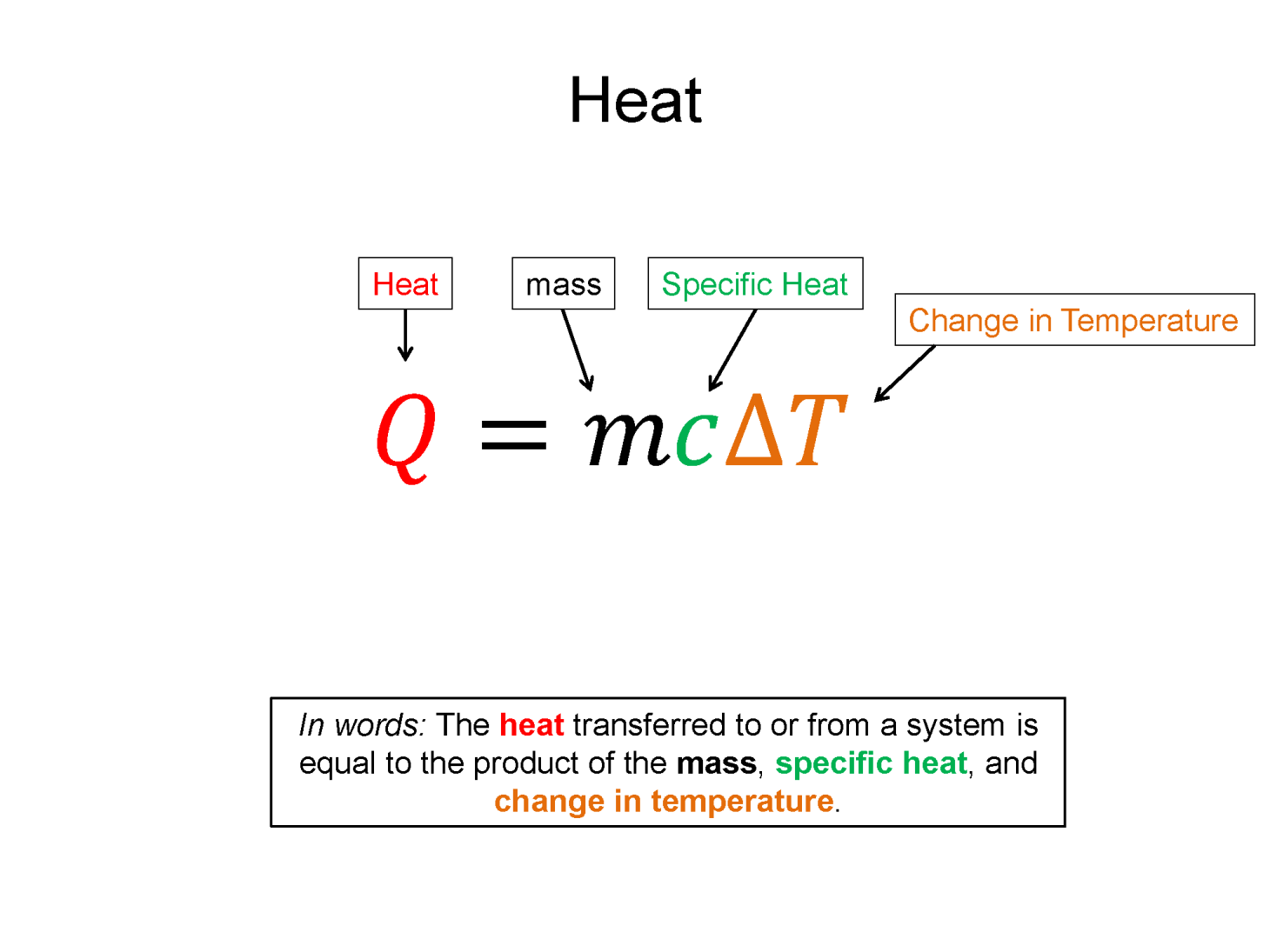
Specific Heat: To increase the temperature of a substance you must add energy. Specific heat (c) is a measure of how much energy (per mass) is required to change a substance a certain temperature, while remaining in a given state (e.g. a liquid).
$c=\frac{1}{m}\frac{\Delta E}{\Delta T}$
The specific heat is a material property since every equal mass substance, when introduced with the same amount of increased energy, would display a different change in temperature. Since energy in these types of experiments is rarely exchanged via work, the form of energy transfer is usually just heat and $\Delta E = Q + W$ reduces to $\Delta E = Q$. With this assumption and a rearrangement of the equation, you get form more often seen in Chemistry. The noted Q equals M C delta T equation.
$Q=mc\Delta T$
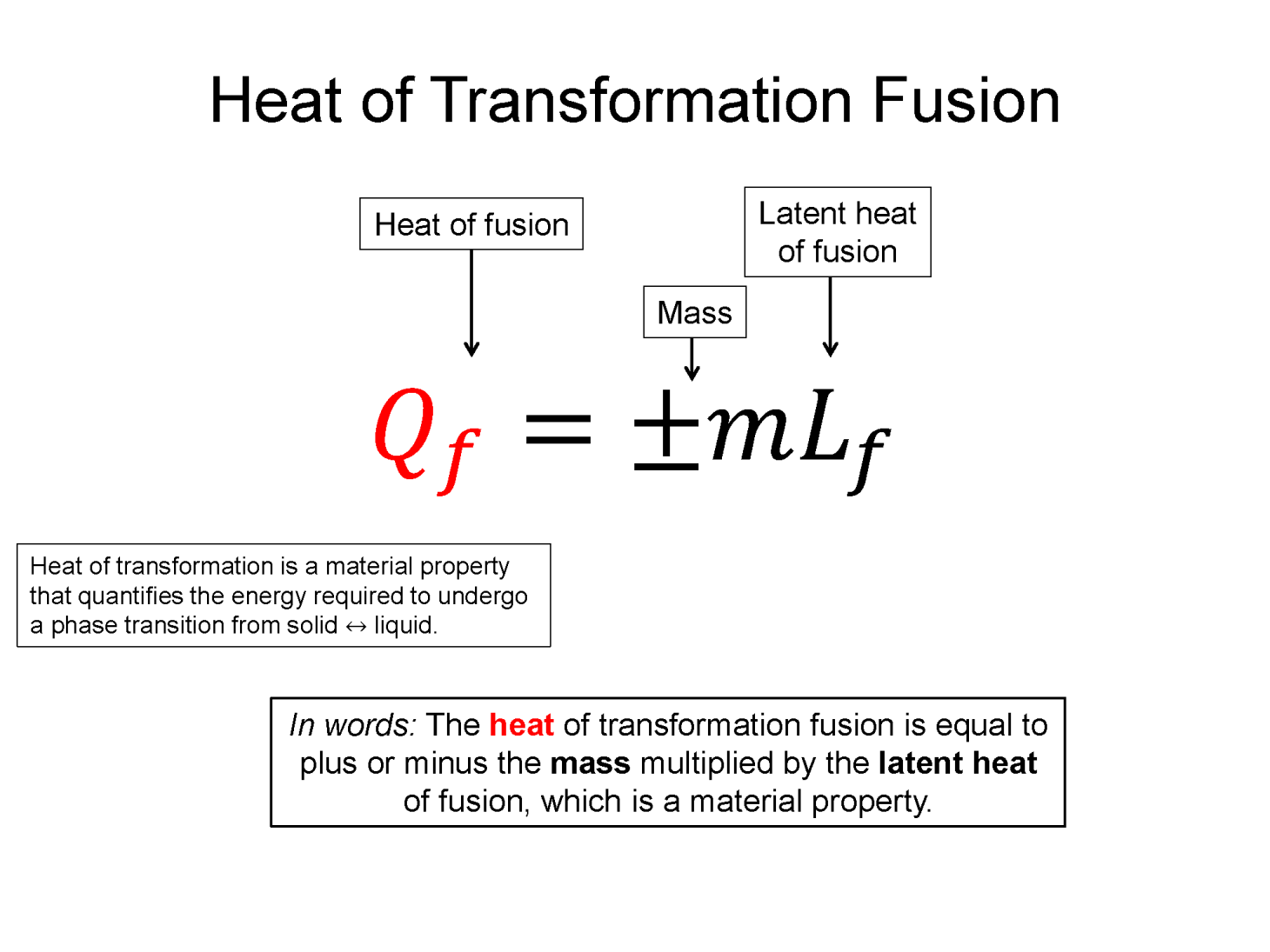
Latent Heat of Transformation: If you where to place a thermometer in a sealed container of very cold (-20 C) ice and heated that container up, you'd see that temperature would increase until it reached 0 C, where while still in solid form, it would begin to change phase into a liquid. This phase transformation from a solid (ice) to a liquid (water) takes time and during that time the system is still increasing its energy, but the temperature doesn't change until all the ice has transformed to water. What this experiment tells you is that it takes energy to change the phase of the system but the temperature does not chance during that transition. Microscopically this means you must put energy into the system to break the bonds holding the molecules tightly together in the solid form, but that energy only goes into the phase transformation and not into the microscopic kinetic energy (temperature). Heat of transformation is a quantification of this energy required to go across a phase transition and it is also a property of the material.
Heat of Fusion (solid <=> liquid), $Q_f = \pm m L_f$
Heat of Vaporization (liquid <=> gas), $Q_v = \pm m L_v$
Here Lf and Lv are transformation properties of the material and the +/- is chosen by whether it's a liquid to gas or a gas to liquid transform.
Calorimetry: A non-SI unit for energy is the Calorie and that is the root of the term calorimetry. Calorimetry is an application of conservation of energy. Calorimetry experiments involve putting two (or more) substances in an isolated container. Isolated means they cannot exchange any energy with the environment, but that can exchange energy between each other. Heat will transfer from the hotter substance to the colder substance until the two reach equilibrium, somewhere in between their initial temperatures. Since the total change of energy of the system must be zero, we can setup an energy expression using the energy transfers during a single phase ($Q=mc\Delta T)$ and the energy transfer for any phase transitions ($Q_f$ or $Q_v$).
$\sum Q = 0$, or $Q_1+Q_2+... = 0$
An example might be putting a hot stone into water and after equilibrium, the whole system is warmer but no steam was generated. Here there are no phase transitions so the $mc\Delta T$ of the stone must be equal and opposite to the $mc \Delta T$ of the water.
$Q_{stone}+Q_{water} = 0$, or $(mc\Delta T)_{stone}+(mc \Delta T)_{water}=0$
Now if the stone had been hot enough to not only increase the water temp up to the boiling point but also turn it into steam, there would an additional term for the phase transition of the water.
$Q_{stone}+Q_{water}+Q_{v,water} = 0$, or $(mc\Delta T)_{stone}+(mc \Delta T)_{water}+(mL_v)_{v, water}=0$
This expression could be used to find the specific heat of the stone, if initial and final temps as well as the mass and specific heat of the water was known. I use this in brewing to calculate what the final temperature of hot water mixed with cold grains will be so that I get the desired final temp.
Key Equations and Infographics
A representation with the words heat on the top. There is an equation that shows that the heat transferred to or from a system is equal to the product of the mass, specific heat, and change in temperature.
A representation with the words specific heat on the top. There is an equation that shows that the specific heat is equal to one over mass multiplied by the change in energy divided by the change in temperature.
A representation with the words heat of transformation fusion on the top. There is an equation that shows that the heat of transformation fusion is equal to plus or minus the mass multiplied by the latent heat of fusion, which is a material property.
A representation with the words heat of vaporization fusion on the top. There is an equation that shows that the heat of transformation vaporization is equal to plus or minus the mass minus the mass multiplied by the latent heat of fusion, which is a material property.
Now, take a look at the pre-lecture reading and videos below.
